Tugas
Pendahuluan 2.
PRAKTIKUM
METODE NUMERIK
OLEH
LUH PUTU SUCI VANDASARI
F1A113054
KELAS A
JURUSAN MATEMATIKA
PROGRAM STUDI MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU
PENGETAHUAN ALAM
UNIVERSITAS HALU OLEO
2014
SOAL.
1. Cari
materi tentang galat dan cara menghitungnya!
2. Cari
materi tentang percabangan if…, if…else,…else!
3. Dengan
cara menentukan nilai akar menggunakan metode bagi 2
Interval (a,b) tentukan sendiri, dan cari galatnya.
PENYELESAIAN.
1. Galat
Ø Pengertian
Penyelesaian
secara numerik dari suatu persamaan matematik hanya memberikan nilai perkiraan
(hampiran) yang mendekati nilai eksak (yang sebenarnya) dari penyelesaian
analitis. Berarti dalam penyelesaian numerik tersebut terdapat galat (error) terhadap
nilai eksak.
Ada
tiga macam galat:
a. Galat
bawaan, terjadi karena kekeliruan dalam menyalin data, salah membaca skala,
atau karena kurangnya pengertian mengenai hukum-hukum .sik dari data yang
diukur.
b. Galat
pembulatan (round-error), terjadi karena tidak diperhitungkannya beberapa
angka terakhir dari suatu bilangan. Sebagai contoh, 3.1415926 dapat dibulatkan
menjadi 3.14.
c. Galat
pemotongan (truncation error), terjadi karena tidak dilakukannya hitungan
sesuai dengan prosedur matematik yang benar. Sebagai contoh, turunan pertama
dari V(t) terhadap t dihitung dengan
prosedur :
Ø Penghitungan
Galat
Untuk galat
pembulatan dan pemotongan, hubungan antara hasil yang eksak dengan hampirannya
dapat dirumuskan :
nilai eksak = hampiran
+ galat
Dengan menyusun
kembali persamaan di atas, diperoleh :
Es = galat = nilai
eksak - hampiran
dimana subskrip s menunjukkan bahwa galat
adalah galat sejati.
Kelemahan
dari denisi di atas adalah bahwa tingkat besaran dari nilai yang diperiksa sama
sekali tidak diperhatikan. Sebagai contoh, galat satu sentimeter jauh lebih
berarti jika yang diukur adalah paku ketimbang jembatan. Salah satu cara untuk
memperhitungkan besarnya besaran yang sedang dievaluasi adalah dengan menormalkan
galat terhadap nilai eksak, yaitu :
Galat relatif
dapat juga dikalikan dengan 100% agar dapat dinyatakan sebagai
Dicatat bahwa
untuk metode numerik, nilai eksak hanya akan diketahui jika fungsi yang ditangani
dapat diselesaikan secara eksak. Jika tidak demikian, maka alternatifnya adalah
menormalkan galat dengan menggunakan hampiran terbaik yang tersedia dari nilai
eksak, yaitu terhadap hampiran itu sendiri, seperti yang dirumuskan :
dengan subskrip h
menunjukkan bahwa galat dinormalkan terhadap nilai hampiran.
2. Materi
percabangan pada MATLAB.
Umumnya
dalam membuat program, selalu ada seleksi dimana diperlukan pengecekan suatu
kondisi untuk mengarahkan program agar berjalan sesuai keinginan. Untuk
melakukan suatu pengecekan kondisi, terdapat tiga macam statemen, yaitu :
a.
Perintah If
Statemen
if digunakan untuk melakukan
penyeleksian dimana jika kondisi bernilai benar maka progam akan mengeksekusi
statemen dibawahnya, setelah penulisan statement diakhiri dengan end. Bentuk
umum perintah if yaitu :
If
kondisi
statemen
end
end
b. Perintah If – Else
Statemen
if – else digunakan untuk melakukan penyeleksian kondisi dimana jika kondisi
bernilai benar maka program akan mengeksekusi statemen 1. Namun, jika nilai
kondisi bernilai salah maka statemen 2 yang akan dieksekusi. Bentuk umum
perintah if – else yaitu :
if
kondisi
statemen
1
else
statemen 2
statemen 2
end
c. Perintah If – Else – Elsif
Statemen if – else -
elsif digunakan untuk melakukan penyeleksian kondisi dimana kondisi yang
diberikan lebih dari 1 kondisi atau memiliki beberapa kondisi. Jika kondisi
pertama bernilai benar maka lakukan seleksi kondisi ke-dua dan seterusnya.
Bentuk umum perintah if – else – elsif yaitu :
if
kondisi1
Statemen
elsif
kondisi2
statemen
else
statemen
end
Dalam interval [1,2] terdapat f(xn)=0
| x | f(x) |
1
|
-2
|
1.1
|
-1.79
|
1.2
|
-1.56
|
1.3
|
-1.31
|
1.4
|
-1.04
|
1.5
|
-0.75
|
1.6
|
-0.44
|
1.7
|
-0.11
|
1.8
|
0.24
|
1.9
|
0.61
|
2
|
1
|
Iterasi
1:
Iterasi 2 : Diamati bahwa
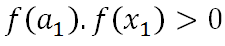
maka :
Iterasi 3 : Diamati bahwa
maka :
Iterasi 4 : Diamati bahwa
maka :
Iterasi 5 : Diamati bahwa
maka :
Iterasi 6 : Diamati bahwa
maka :
Iterasi 7 : Diamati bahwa
maka :
Jadi, pada iterasi ke-7 diperoleh akar hampiran
Iterasi 5 : Diamati bahwa
maka :
Iterasi 6 : Diamati bahwa
maka :
Iterasi 7 : Diamati bahwa
maka :
Jadi, pada iterasi ke-7 diperoleh akar hampiran
dengan
galat (error) 0.5%.




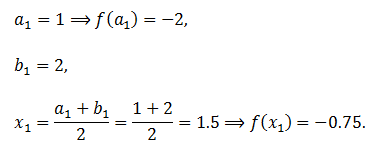












Tidak ada komentar:
Posting Komentar